LANGUAGES
Our concept of language is an abstraction of the concept of a
natural language.
LANGUAGE CONCEPTS AND NOTATION
- alphabet, denoted by
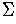
- a nonempty set of symbols
By convention, we use lowercase letters a, b, c, ...
to represent elements of
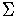 .
.
For example,
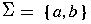
- strings
- finite sequences of symbols from the alphabet
By convention, we use lowercase letters ..., u, v, w, x, y, z
to represent strings.
For example,
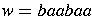 is a string from the above alphabet.
is a string from the above alphabet.
- concatenation of strings u and
v
- appending the symbols of v to the right end (i.e.,
after) the symbols of u, denoted by uv
If
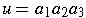 and
and
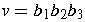 , then
, then
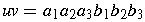
- associativity of string concatenation
-
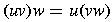
Thus normally just write uvw without parentheses.
- string concatenation is not commutative.
- That is,
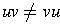 .
.
- reverse of a string w, denoted by
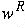 .
.
- string with same symbols, but with the order reversed
If
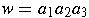 , then
, then
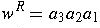 .
.
- length of a string w, denoted by
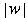
- the number of symbols in string w
- empty string, denoted by
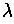
- the string with no symbols,
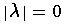
The empty string is the identity element for
concatenation,
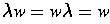
FORMAL INTERLUDE: INDUCTIVE DEFINITIONS AND INDUCTION
- Inductive Definition of Length
- Note: differs from textbook -- here begin with the empty string
-
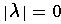
-
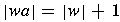
Using the fact that
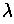 is the identity element and the above
definition:
is the identity element and the above
definition:
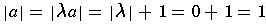
- Prove:
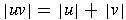
-
- Noting the definition of length above, we choose to do an
induction over string v (or, if you prefer, over the length
of
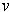 , basing induction at 0):
, basing induction at 0):
- Base case
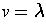 (that is, length is 0)
(that is, length is 0)
-
| |
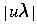
|
| = | { identity for concatenation } |
| |
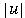
| |
| = | { identity for + } |
| |
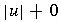
| |
| = | { definition of length } |
| |
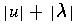
| |
- Inductive case
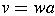 (that is, length is greater than 0)
(that is, length is greater than 0)
- induction hypothesis:
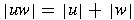
-
| |
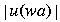
|
| = | { associativity of concatenation } |
| |
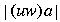
| |
| = | { definition of length } |
| |
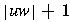
| |
| = | { induction hypothesis } |
| |
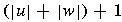
| |
| = | { associativity of + } |
| |
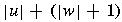
| |
| = | { definition of length (right to left)} |
| |
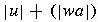
| |
Thus we have proved
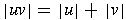
LANGUAGE CONCEPTS AND NOTATION (CONTINUED)
- substring of a string w
- any string of consecutive symbols in w
If
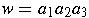 , then the substrings
are
, then the substrings
are
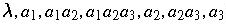 .
.
If w = vu, then v is a prefix of
w; u is a suffix.
If
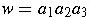 , then the prefixes
are
, then the prefixes
are
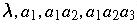 .
.
-
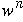 , for any string w and
, for any string w and
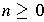
- denotes n repetitions of string (or symbol) w
-
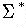 , for alphabet
, for alphabet
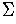
- denotes the set of all strings obtained by concatenating zero
or more symbols from the alphabet
-
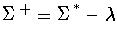
- language
- a subset of
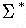 , for some alphabet
, for some alphabet
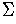
- sentence of some language L
- any string from L (i.e., from
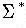 )
)
Example Languages
Let
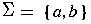 .
.
-
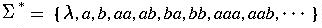 .
.
-
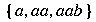 is a language on
is a language on
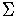 .
.
Since the language has a finite number of sentences, it is a
finite language.
-
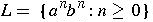 is also a language on
is also a language on
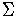 .
.
Sentence aabb and aaaabbbb are in L, but
aaabb is not.
As with most interesting languages, L is
an infinite language.
OPERATIONS ON LANGUAGES
Languages are represented as sets. Operations on languages can be
defined in terms of set operations.
- union, intersection, and
difference
- directly as matching operations on sets
- complementation with respect to
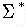
-
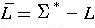
- reverse
-
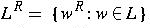 -- reverse all strings
-- reverse all strings
- concatenation
-
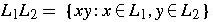
-
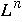
- L concatenated with itself n times
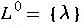 and
and
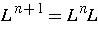
- star-closure
-
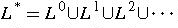
- positive closure
-
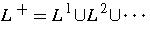
Language Operation Examples
Let
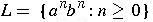 .
.
-
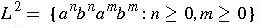 (where n and m are unrelated).
(where n and m are unrelated).
-
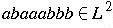 .
.
-
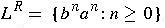
How would we express in
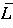 and
and
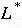 ?
?
Although set notation is useful, it is not a convenient notation for
expressing complicated languages.
[Next]
Copyright © 1999, H. Conrad Cunningham
Last modified: Sun Aug 22 18:40:35 CDT 1999
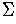
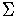 .
.
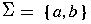
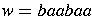 is a string from the above alphabet.
is a string from the above alphabet.
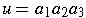 and
and
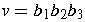 , then
, then
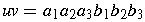
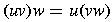
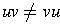 .
.
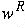 .
.
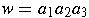 , then
, then
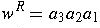 .
.
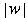
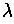
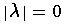
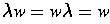
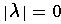
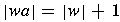
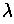 is the identity element and the above
definition:
is the identity element and the above
definition: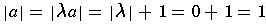
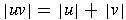
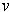 , basing induction at 0):
, basing induction at 0):
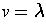 (that is, length is 0)
(that is, length is 0)
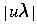
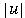
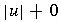
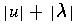
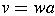 (that is, length is greater than 0)
(that is, length is greater than 0)
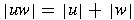
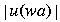
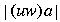
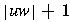
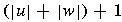
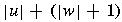
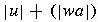
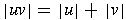
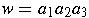 , then the substrings
are
, then the substrings
are
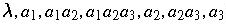 .
.
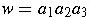 , then the prefixes
are
, then the prefixes
are
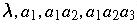 .
.
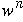 , for any string w and
, for any string w and
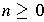
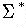 , for alphabet
, for alphabet
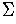
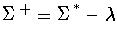
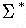 , for some alphabet
, for some alphabet
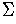
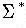 )
)
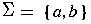 .
.
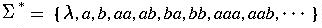 .
.
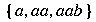 is a language on
is a language on
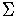 .
.
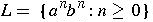 is also a language on
is also a language on
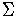 .
.
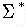
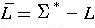
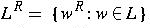 -- reverse all strings
-- reverse all strings
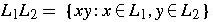
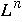
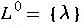 and
and
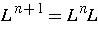
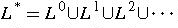
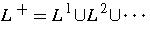
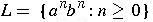 .
.
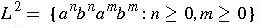 (where n and m are unrelated).
(where n and m are unrelated).
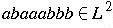 .
.
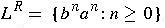
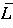 and
and
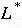 ?
?