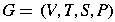 where
where
- V is a finite set of objects called
variables.
- T is a finite set of objects called
terminal symbols.
-
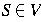 is a special symbol called the start
symbol.
is a special symbol called the start
symbol.
- P is a finite set of productions.
- V and T are nonempty and disjoint.
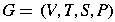 where
where
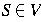 is a special symbol called the start
symbol.
is a special symbol called the start
symbol.
Productions have form
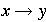 where
where
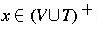 , i.e., x is some non-null string
of terminals and variables
, i.e., x is some non-null string
of terminals and variables
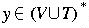 , i.e.,
y is some, possibly null, string of terminals and variables
, i.e.,
y is some, possibly null, string of terminals and variables
Application of productions, given
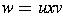 :
:
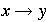 is applicable to string w
is applicable to string w
New string
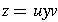 :
:
w derives z,
written
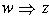
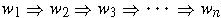
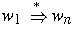
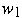 derives
derives
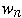 in zero or more production steps.
in zero or more production steps.
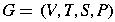 be a grammar.
Then
be a grammar.
Then
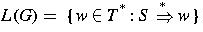 is the language generated by G.
is the language generated by G.
That is, L(G) is the set of all strings that can be generated from the start symbol S using the productions P.
A derivation of some sentence
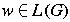 is a sequence
is a sequence
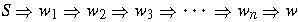
The strings
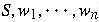 above are sentential
forms of the derivation of sentence w.
above are sentential
forms of the derivation of sentence w.
Consider
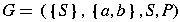 where P is
where P is
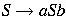
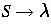
Consider
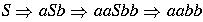 ,
hence,
,
hence,
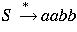 .
.
aabb is a sentence of the language; the other strings in the derivation are sentential forms.
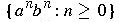
Usually, however, it is difficult to construct an explicit set definition of a language generated by a grammar.
Now prove the conjecture.
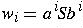 for
for
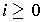 by induction on i.
by induction on i.
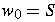 is a sentential form, the start symbol.
is a sentential form, the start symbol.
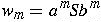 is a sentential form, show that
is a sentential form, show that
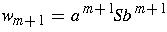 .
.
Case 1: If we begin with the assumption and apply production
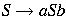 , we get sentential form
, we get sentential form
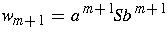 .
.
Case 2: If we begin with the assumption and apply production
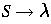 , we get the sentence
, we get the sentence
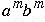 rather than
a sentential form.
rather than
a sentential form.
Hence, all sentential forms have the form
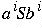 .
.
Given that
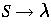 is the only production with
terminals on the right side, we must apply it to derive any sentence.
As we noted in case 2 above, application of the production to any
sentential form gives a sentence of the form
is the only production with
terminals on the right side, we must apply it to derive any sentence.
As we noted in case 2 above, application of the production to any
sentential form gives a sentence of the form
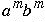 .
.
Given
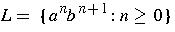 .
.
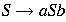 would generate sentential
forms
would generate sentential
forms
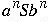 .
.
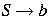 .
.
A slightly different grammar might introduce nonterminal A as follows:
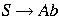
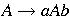
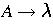
To show that a language L is generated by a grammar G, we must prove:
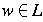 , there is a derivation using G.
, there is a derivation using G.
Two grammars are equivalent if they generate the same language.
For example, the two grammars given above for the language
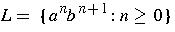 are equivalent.
are equivalent.