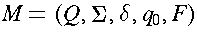 where
where
- Q is a finite set of internal states.
-
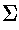 is a finite set of symbols called the input
alphabet.
is a finite set of symbols called the input
alphabet.
-
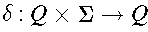 is a total function
called the transition function.
is a total function
called the transition function.
-
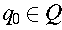 is the initial state.
is the initial state.
-
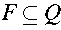 is a set of final states.
is a set of final states.
Reference: This material is based on section 2.1 of the Linz textbook.
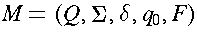 where
where
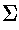 is a finite set of symbols called the input
alphabet.
is a finite set of symbols called the input
alphabet.
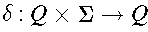 is a total function
called the transition function.
is a total function
called the transition function.
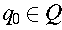 is the initial state.
is the initial state.
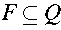 is a set of final states.
is a set of final states.
A dfa operates as follows:
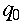
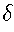 (currentState,currentInput)
(currentState,currentInput)
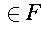 then ACCEPT else REJECT
then ACCEPT else REJECT
To visualize a dfa, we use a transition graph
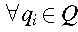
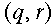 with label
with label
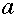 if and only if
if and only if
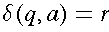
See Example 2.1 in Linz textbook.
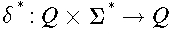 is defined recursively:
is defined recursively:
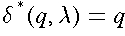
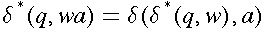
The extended transition function gives the state of the automaton after reading a string.
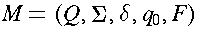
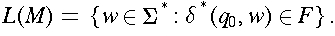
That is, L(M) is the set of all strings on the input alphabet accepted by automaton M.
Note that above
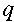 and
and
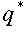 are total functions (defined
for all strings).
are total functions (defined
for all strings).
See example 2.2 in the Linz textbook.
A trap state is a state from which the automaton can never "escape".
Transition graphs are quite convenient for understanding finite automata.
For other purposes--such as representing finite automata in
programs-- a tabular representation of transition function
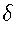 may also be convenient.
may also be convenient.
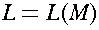 .
.
Dfas define the family of languages called regular.
See examples in the Linz textbook.