- alphabet, denoted by
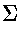
- a nonempty set of symbols
By convention, we use lowercase letters a, b, c, ...
to represent elements of
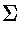 .
.
For example,
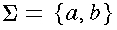
- strings
- finite sequences of symbols from the alphabet
By convention, we use lowercase letters ..., u, v, w, x, y, z
to represent strings.
For example,
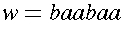 is a string from the above alphabet.
is a string from the above alphabet.
- concatenation of strings u and
v
- appending the symbols of v to the right end (i.e.,
after) the symbols of u, denoted by uv
If
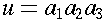 and
and
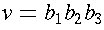 , then
, then
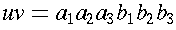
- reverse of a string w, denoted by
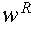 .
.
- string with same symbols, but with the order reversed
If
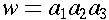 , then
, then
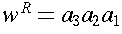 .
.
- length of a string w, denoted by
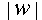
- the number of symbols in string w
- empty string, denoted by
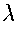
- the string with no symbols,
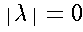
The empty string is the identity element for
concatenation,
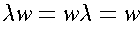
- substring of a string w
- any string of consecutive symbols in w
If
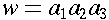 , then the substrings
are
, then the substrings
are
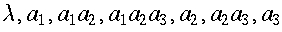 .
.
If w = vu, then v is a prefix of
w; u is a suffix.
-
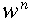 , for any string w and
, for any string w and
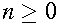
- denotes n repetitions of string (or symbol) w
If
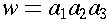 , then the prefixes
are
, then the prefixes
are
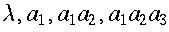 .
.
-
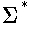 , for alphabet
, for alphabet
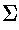
- denotes the set of all strings obtained by concatenating zero
or more symbols from the alphabet
-
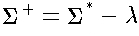
- language
- a subset of
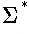 , for some alphabet
, for some alphabet
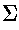
- sentence of some language L
- any string from L (i.e., from
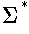 )
)
Languages are represented as sets. Operations on languages can be
defined in terms of set operations.
Although set notation is useful, it is not a convenient notation for
expressing complicated languages.
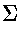
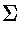 .
.
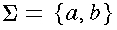
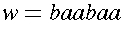 is a string from the above alphabet.
is a string from the above alphabet.
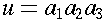 and
and
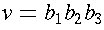 , then
, then
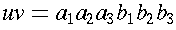
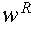 .
.
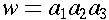 , then
, then
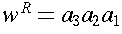 .
.
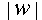
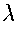
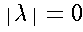
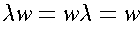
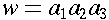 , then the substrings
are
, then the substrings
are
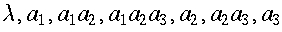 .
.
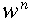 , for any string w and
, for any string w and
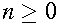
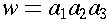 , then the prefixes
are
, then the prefixes
are
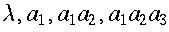 .
.
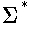 , for alphabet
, for alphabet
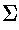
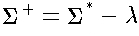
 , for some alphabet
, for some alphabet
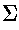
 )
)
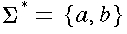 .
.
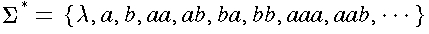 .
.
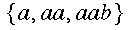 is a language on
is a language on
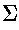 .
.
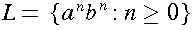 is also a language on
is also a language on
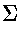 .
.
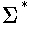
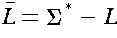
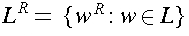 -- reverse all strings
-- reverse all strings
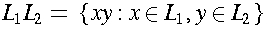
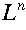
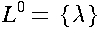 and
and
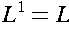
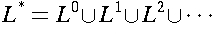
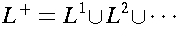
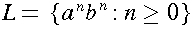 .
.
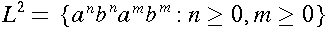 (where n and m are unrelated).
(where n and m are unrelated).
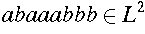 .
.
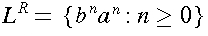
 and
and
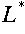 ?
?